|
Finanzmathematik
Inhaltsübersicht
I. Anwendungsgebiete
II. Zahlungsfolgen und -reihen als Grundlagen finanzmathematischer Methoden
III. Zinsrechnung
IV. Tilgungsrechnung
V. Rentenrechnung
VI. PC-Anwendungen
I. Anwendungsgebiete
Die Finanzmathematik stellt ein Teilgebiet der angewandten Mathematik dar. Das Spektrum der Anwendungen umfasst schwergewichtig Fragen zur Investitions- und Finanzierungsrechnung (Zins-, Tilgungs- und Rentenrechnung, Kurs- und Renditebestimmung, Zielwertermittlung von Investitionsprojekten) und zur Versicherungsmathematik (Spezialanwendungen der Wahrscheinlichkeitstheorie). Außerdem ist die Darstellung von Abschreibungsmethoden Gegenstand der Finanzmathematik. Die folgenden Ausführungen beschränken sich auf das Gebiet der Finanzierungsrechnung.
Zur Lösung finanzmathematischer Fragestellungen werden grundsätzlich Formeln mit Bildungsgesetzen verwendet, die letztlich auf Zahlenfolgen und -reihen zurückzuführen sind.
II. Zahlungsfolgen und -reihen als Grundlagen finanzmathematischer Methoden
1. Zahlenfolgen
Eine Zahlenfolge stellt eine durch Indexelemente geordnete Aneinanderreihung reeller Zahlen dar. Formal kann die Zahlenfolge wie folgt beschrieben werden: a1,a2,...,ai,... . Die Zahlenfolge kann endlich oder unendlich sein. Sie wird entweder unmittelbar vorgegeben (z.B. die gezogenen Elemente bei einer Lotterie) oder durch ein mathematisch formuliertes Bildungsgesetz bestimmt (z.B. die exponentiell steigende Entwicklung einer Variablen im Zeitablauf). Bezüglich der Verlaufsrichtung sind steigende, fallende und konstante Zahlenfolgen zu unterscheiden.
Ist die Differenz zwischen beliebigen aufeinanderfolgenden Elementen einer Zahlenfolge konstant, so liegt eine arithmetische Folge vor. Das Element ai ergibt sich hierbei wie folgt:
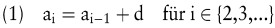
Die arithmetische Zahlenfolge ist durch ihr Anfangsglied a1 und die Differenz d definiert. Der Wert des i-ten Elements ist wie folgt berechenbar:
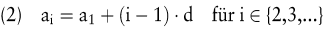
Die Differenz d erlaubt eine Klassifizierung der arithmetischen Zahlenfolge:
d > 0 definiert eine steigende, d < 0 eine sinkende und d = 0 eine konstante Zahlenfolge.
Ergibt sich das Element ai für i ∊ {2,3,...} einer Zahlenfolge aus dem vorhergehenden durch Multiplikation mit einem konstanten Faktor q, so liegt eine geometrische Zahlenfolge vor. Das Bildungsgesetz lautet hierbei:
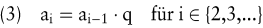
Der Wert eines Elementes einer geometrischen Zahlenfolge kann bei gegebenem Anfangselement a1 und gegebenem Faktor q wie folgt bestimmt werden:
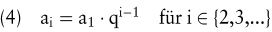
Die Summe S der ersten n Elemente einer Zahlenfolge wird als Zahlenreihe bezeichnet:
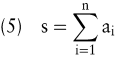
Bei Vorliegen einer arithmetischen Zahlenfolge mit einer endlichen Anzahl von Elementen kann der Wert S der arithmetischen Reihe durch einige Umformungen in die folgende kompakte Form gebracht werden:
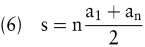
Eine geometrische Zahlenreihe stellt die Summe der ersten n Elemente einer geometrischen Folge dar. Der Wert einer endlichen geometrischen Reihe S wird wie folgt ermittelt:
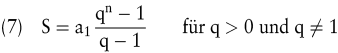
Während arithmetische Folgen und Reihen insbesondere für Abschreibungsmethoden bedeutsam sind, bilden geometrische Folgen und Reihen die Grundlage für die nun darzustellende Zins-, Tilgungs- und Rentenrechnung.
III. Zinsrechnung
1. Standardansätze
Zinsen sind Entgelte für die Zurverfügungstellung von Kapital. Aus der Sicht des Kapitalgebers stellen sie Erträge, aus der des Kapitalnehmers Aufwendungen dar.
Die Zinsen resultieren aus der Höhe und Zeitdauer des zur Verfügung gestellten Kapitals sowie dem Zinssatz und den Modalitäten der Zinsverrechnung. Für den Standardansatz wird angenommen, dass das zu Beginn des Kreditzeitraums aufgenommene Kapital erst am Ende der Laufzeit getilgt wird. Eine Variation des gebundenen Kapitals wird im Rahmen der Tilgungsrechnung behandelt.
Bezüglich der Zeitdauer kann eine jährliche, mehrjährige oder unterjährige Verzinsung erfolgen, deren Grenzfall die Momentanverzinsung ist. Im Hinblick auf die Kapitalisierung der Zinsen ist zwischen der Verrechnung von Zinseszinsen, einfacher ( „ bürgerlicher “ ) Verzinsung und gemischter Verzinsung zu unterscheiden. Der Verrechnung von Zinseszinsen kommt die größte praktische Bedeutung zu. Sie soll deshalb im Folgenden weiter ausgeführt werden.
Die jährliche Verzinsung des Kapitals K zum Zinsfuß i führt zu folgenden Zinsen Z:
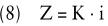
Diese Formel stellt gleichzeitig die Ausgangsformel für die mehrjährige und die unterjährige Betrachtung dar. Bei einer mehrjährigen Betrachtung sind die am Ende eines Jahres anfallenden Zinsen dem Kapital gutzuschreiben. Sie erhöhen damit den Ausgangsbetrag zur Berechnung der Zinsen des Folgejahres.
Das Kapital am Ende des ersten Jahres K1 ergibt sich dann wie folgt:
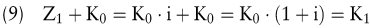
Allgemein gilt:
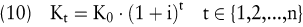
Bei unterjähriger Verzinsung werden die Zinsen mindestens zweimal innerhalb eines Jahres kapitalisiert. Wenn die Verrechnung der Zinsen in gleichen zeitlichen Distanzen erfolgt (z.B. halbjährlich), kann die Berechnung durch eine Formel vorgenommen werden. Ansonsten ist das Aufstellen eines Finanzplans erforderlich.
Die Formel zur Berechnung der Zinsen bei unterjähriger Verzinsung kann mit dem Periodenzinssatz ip entwickelt werden. Hierbei ist zu berücksichtigen, dass die Zinsen am Ende der ersten Zinsperiode (k=1) des ersten Jahres (t=1) sich wie folgt ergeben:
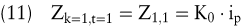
Das Kapital beträgt mithin:
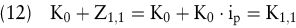
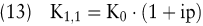
Am Ende des Jahres n beträgt das Kapital bei m unterjährigen Zinsperioden
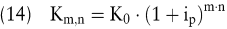
Allgemein nimmt das Kapital zum Ende der k-ten Zinsperiode des Jahres t folgende Höhe an:
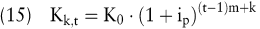
Die unterjährige Verzinsung wird zum sogenannten relativen Zinssatz vorgenommen, der sich wie folgt aus dem nominellen Jahreszinssatz inom ergibt: inom/m.
Wegen der unterjährigen Zinseszinseffekte ist der nominelle Jahreszinssatz inom niedriger als der effektive Jahreszinssatz ieff. ieff kann aufgrund der folgenden Gleichgewichtsbedingung errechnet werden:
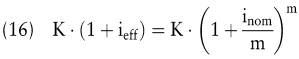
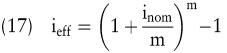
Wenn der nominelle Jahreszinssatz als effektiver Jahreszinssatz gewählt werden soll, wird der unterjährige Zinssatz als konform bezeichnet. ikon ergibt sich aufgrund der folgenden Ausgangsgleichung:
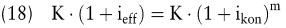
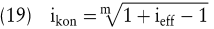
In bestimmten Modellen (z.B. bei der klassischen Theorie der optimalen Nutzungsdauer auf Basis stetig verlaufender Zahlungsströme) ist die Ermittlung einer Momentanverzinsung bedeutsam (Hax, H. 1993; Perridon, /Steiner, 1999). Die Verzinsung des Kapitals „ in jedem Moment “ – auch als stetige Verzinsung bezeichnet – macht Grenzwertbetrachtungen erforderlich.
Ausgangspunkt zur Herleitung der Momentanverzinsung ist die Formel zur Bestimmung des Kapitals am Endes des ersten Jahres bei unterjähriger Verzinsung zum relativen Zinssatz inom/m.
Für inom wird im Folgenden das Symbol i verwendet.
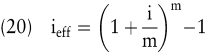
Nach Ersetzen von i/m durch 1/x wird eine Grenzwertbetrachtung durchführt, deren Ergebnis die Eulersche Zahl e ist:
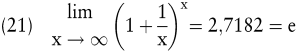
Als Kapital zum Ende des ersten Jahres ergibt sich für den Fall einer Momentanverzinsung
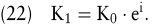
Für eine n-jährige Kapitalanlage gilt:
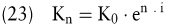
Der effektive Jahreszinsfuß bei stetiger Verzinsung kann aufgrund der folgenden Ausgangsgleichung errechnet werden:
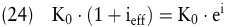
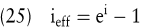
Bei Entscheidungssituationen, die nicht den durch finanzmathematische Bildungsgesetze charakterisierbaren Standardansätzen entsprechen, ist anstelle der formelorientierten eine finanzplanorientierte Problemlösung vorzunehmen. Dies ist insbesondere bei der Investitions- und Finanzplanung der Fall, bei der die Konditionenvielfalt auf den Finanzierungssektor sowie die steuerlichen Konsequenzen im Modell abzubilden sind. Die finanzplanorientierte Methode wird durch Tabellenkalkulationsverfahren praktikabel.
2. Erweiterung der Standardansätze
Die Bestimmung des Kapitals nach Ablauf der Kredit- oder Anlagedauer erfolgt in Bezug auf seine nominelle Höhe. Aus Sicht des Entscheidungsträgers sind im Allgemeinen steuerliche Effekte zu berücksichtigen, da ein Zinsertrag (Zinsaufwand) die steuerliche Bemessungsgrundlage für die Errechnung der Ertragsteuern erhöht (mindert).
Im Falle von Kapitalanlagen ergibt sich bei jährlicher Zinsgutschrift ein um die zurechenbaren Ertragsteuern S1 korrigiertes Kapital von:
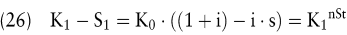
Hierbei stellt s den konstanten marginalen Ertragsteuersatz dar. Die Formel kann wie folgt verkürzt werden:
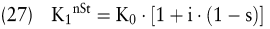
Bei mehrjähriger Kapitalbindung lässt sich das Kapital am Ende des Jahres t unter Berücksichtigung einer jährlichen Steuerzahlung wie folgt bestimmen:
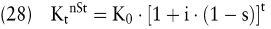
Bei dieser Analyse werden sämtliche der Kapitalanlage kausal zurechenbaren Steuerzahlungen zeitgleich mit den Zinsgutschriften erfasst.
Bei einem Kredit fällt bei Abzugsfähigkeit der Zinsen eine „ Steuergutschrift “ an. Hierbei wird unterstellt, dass eine Kompensation mit einer positiven Bemessungsgrundlage aus weiteren Einkünften des Steuerpflichtigen besteht.
Bei unterjähriger Verzinsung ist zunächst anzunehmen, dass zwar die Zinsgutschrift mehrfach im Laufe eines Jahres, die Steuerzahlung für die Zinsen, die als Differenz des Kapitals am Ende und am Anfang des Jahres errechenbar sind, jedoch einmalig am Ende des Jahres erfolgt. Für eine Kapitalanlage kann folgende Formel konstruiert werden:
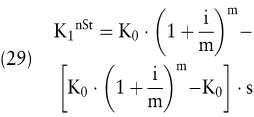
Im Falle einer Kreditfinanzierung können durch die Zinsen „ Steuergutschriften “ verursacht werden.
Bei einer komplexeren Entscheidungssituation (z.B. bei mehrjähriger Betrachtung unter Berücksichtigung von time lags bei den Steuerzahlungen) empfiehlt sich die Darstellung der Daten in einem VOFI (VOFI = Akronym für vollständige Finanzplanung).
Als Beispiel sei eine Kapitalanlage von 10.000 EUR zu einem relativen Zinssatz von 2%, quartalsweiser Zinsgutschrift und einer Laufzeit von 2 Jahren dargestellt. Folglich ist der Zinsfaktor q = 1,02. Der marginale Ertragsteuersatz betrage 60%. Die Steuerzahlung erfolge am 30.06. des Folgejahres auf Basis der Zinseinkünfte des Vorjahres. In diesem Fall ergibt sich die folgende Rechnung, bei der zwischen der nominellen Entwicklung des Kapitalkontos und dem Projekt, dem sämtliche verursachungsgerecht zurechenbaren Zahlungen rechnerisch zugeordnet werden, zu unterscheiden ist. 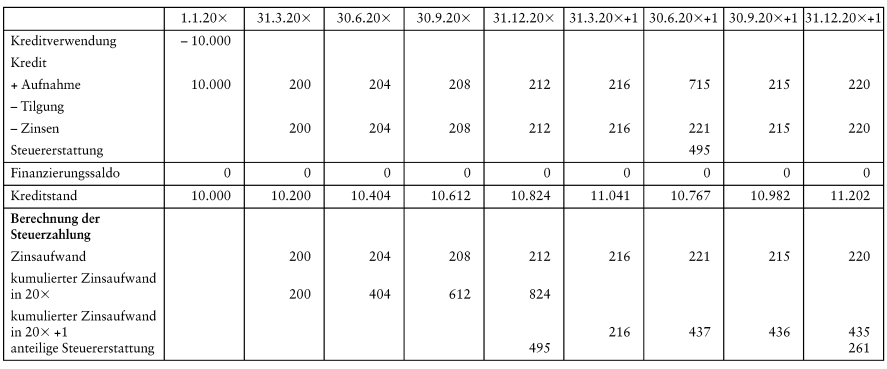
Abb. 1: Kapitalentwicklung unter Berücksichtigung von Steuern
Der Wertansatz am 31.12.20x+1 ist unter Berücksichtigung der auf diesen Planungshorizont abzuzinsenden Steuerzahlung vom 30.06.20x+2 wie folgt zu bestimmen:
11.202,03 – 872,30 · 0,6 · [1 + 0,02· (1 – 0,6)]-2 = 10.686,92 [EUR]
Selbstverständlich ist auch die Entwicklung einer Formel zur Abbildung der Entscheidungssituation möglich. Der entsprechende Ausdruck zur Bestimmung des projektbezogenen Kapitals in n=2 setzt sich aus dem Kapital ohne Steuern sowie aus den aufgezinsten Steuerzahlungen auf die Zinsen in t=1 zusammen. Die Steuerzahlung erfolgt im Zeitpunkt τ. τ stellt den Index für das Quartal dar: τ ∊ {1,...,n · m}. Die Formel für den Kapitalbestand des Projektes ohne Berücksichtigung der Steuerzahlungen in 20x+2 lautet:
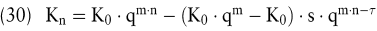
Wegen der Individualität der Datensituation mag die formelmäßige Bestimmung jedoch nicht als zweckmäßig angesehen und einer finanzplanorientierten Entwicklung der Vorzug eingeräumt werden.
IV. Tilgungsrechnung
1. Die Konditionenvielfalt
Bei der Vereinbarung der Konditionen eines Kredits sind dessen Tilgungsmodalitäten festzulegen. Hierbei ist die Liquiditätswirkung aus der Sicht des Kreditgebers bzw. -nehmers zu beachten. Bei laufenden Krediten (Kontokorrentkrediten) sind Aufnahme und Tilgung je nach Liquiditätsbedarf im Rahmen eines vertraglich vereinbarten Kreditspielraums möglich. In der Finanzmathematik werden jedoch nur Kredite mit regelmäßiger Tilgung betrachtet. Während bei Krediten mit endfälliger Tilgung während der Laufzeit lediglich Zinszahlungen zu entrichten sind, fallen bei der Raten- und Annuitätentilgung Zins- und Tilgungsbeträge zu festgelegten Zeitpunkten und in festgelegter Höhe innerhalb der Kreditlaufzeit an. Für den Raten- und den Annuitätenkredit können tilgungsfreie Laufzeiten vereinbart werden.
2. Ausgewählte Tilgungsmodalitäten a) Ratentilgung
Der Ratenkredit ist durch konstante Tilgungsbeträge innerhalb des Tilgungszeitraums gekennzeichnet. Im Folgenden wird von einem Kredit mit mehrjähriger Laufzeit ausgegangen. Unter der Voraussetzung einer jährlich nachschüssigen Zinszahlung und Tilgung ergibt sich für die tilgungsfreie Zeit t ∊ {1,...,f} eine konstante Liquiditätsbelastung in Höhe der Zinsen auf den Nennwert des Kredites B0.
Im Tilgungszeitraum t ∊ {t+1,...,n} sinkt die Zinsbelastung aufgrund der konstanten Reduktion der Kapitalbindung in Höhe der Tilgung T.


Betrachtet man nicht nur die nominelle Entwicklung des Kreditkontos, sondern bildet sämtliche durch den Kredit verursachten relevanten Zahlungen in einem projektbezogenen Modell ab, dann sind bei der Liquiditätsbelastung auch die Steuern zu berücksichtigen. Unter der Annahme, dass die Zinszahlungen die Steuerbemessungsgrundlage in voller Höhe mindern, muss bei der Ermittlung der jährlichen liquiditätsmäßigen Belastung der steuerkorrigierte Zinssatz i · (1 – s) angesetzt werden.
Zu unterjährigen Varianten eines Ratenkredits vgl. Bosch und Kruschwitz (Bosch, K. 1998; Kruschwitz, L. 1995). b) Annuitätentilgung
Bei der Annuitätentilgung ist die als Annuität bezeichnete Summe von Tilgung und Zinsen während der Tilgungsphase konstant. Falls eine tilgungsfreie Zeit t ∊ {1,...,f} vereinbart wird, sind in dieser Phase lediglich Zinsen zu zahlen.
Für die Tilgungsphase t ∊ {f+1,...,n} wird die Annuität durch Multiplikation des Nennbetrages des Kredits mit dem Annuitätenfaktor errechnet:
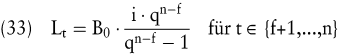
Die Liquiditätsbelastung Lt ist sukzessiv in den Zins- und Tilgungsanteil aufzuspalten. Die Aufspaltung ist insbesondere bei der Einbeziehung der steuerlichen Effekte interessant, da Zinsen die Steuerzahlungen beeinflussen können.
Wenn die dem Zinsaufwand zugerechnete Steuererstattung zeitlich synchron zur Zinszahlung verläuft, ist im Annuitätenfaktor der steuerverkürzte Zinsfuß anzusetzen. Wegen der dem Kreditvorhaben zugerechneten Steuererstattung kann dabei zunächst ein höherer Betrag getilgt werden, als dies bei Vernachlässigung der Steuern möglich ist. Hierdurch wird die Zinsbelastung wegen des Verzichts auf den „ heimlichen Liquiditätseffekt “ aufgrund einer Vernachlässigung der Steuern insgesamt reduziert.
Ein Beispiel mit folgenden Daten möge den Zusammenhang verdeutlichen:
B0 = 12.000; i = 12%; s = 0,6; n = 3
Die Annuität ohne Berücksichtigung von Steuern beläuft sich auf 49.961,88 [EUR/Jahr]. Tilgungsplan sowie Zinszahlungen und Steuererstattungen, sind in der folgenden Abbildung ausgewiesen worden:
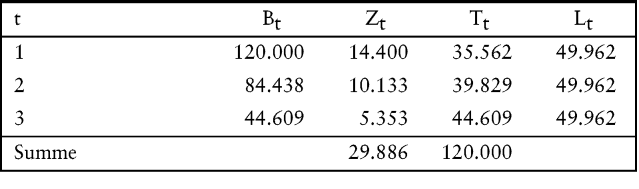
Abb. 2: Berechnung der Annuität ohne Steuern
Aus Abb. 3 geht die nachträgliche Einbeziehung der Steuern St hervor, die zu der Liquiditätsbelastung nach Steuern LnStt führt.
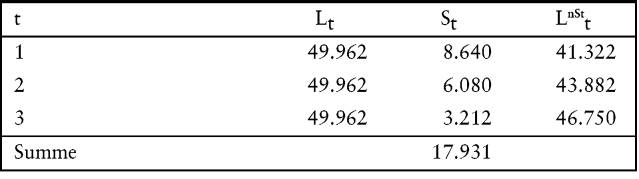
Abb. 3: Nachträgliche Berechnung von Steuern
Unter Berücksichtigung eines steuerverkürzten Zinsfußes bei der Ermittlung der Annuitätentilgung ergeben sich die folgenden Daten:
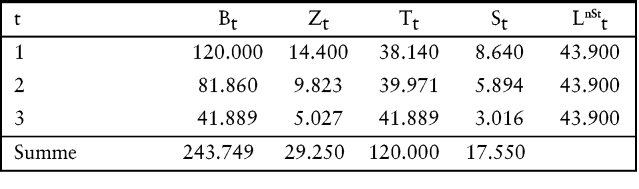
Abb. 4: Berechnung der Annuität mit Steuern
Aus der letzten Spalte von Abb. 4 geht hervor, dass die Liquiditätsbelastung, die bei diesem Ansatz aus dem Kapitaldienst (Tilgung + Zinsen) und der Steuererstattung resultiert, im Zeitablauf konstant ist. Eine Differenzbetrachtung der Liquiditätsbelastungen bei den Annuitätenberechnungen ohne (Abb. 2 und 3) und mit Steuern (Abb. 4) zeigt, dass der „ heimliche Liquiditätseffekt “ bei Vernachlässigung der Steuern nur in der Anfangsphase auftritt und letztlich überkompensiert wird.
Die Auswahl der günstigsten Kreditkonditionen kann nur unter Berücksichtigung des effektiven Reinvestitions- bzw. Refinanzierungssatzes, der bei der Disposition der alternativen Liquiditätsbelastungen anzusetzen ist, getroffen werden (Grob, H. L. 2001). c) Weitere Ansätze
In der Literatur werden zahlreiche Varianten der hier dargestellten Standardansätze (z.B. unterjährige Tilgung und jährliche Zinszahlungen) diskutiert (Bosch, K. 1998; Kruschwitz, L. 1995).
V. Rentenrechnung
1. Klassifizierung und Fragestellungen
Der finanzmathematische Begriff Rente ist durch regelmäßige Zahlungen zu äquidistanten Zeitpunkten charakterisierbar. Die Höhe der Zahlung ist grundsätzlich konstant. Bei einer Variation der Zahlungen im Zeitablauf wird im Allgemeinen nur dann von einer Rente gesprochen, wenn die zeitliche Entwicklung einem finanzmathematischen Bildungsgesetz (z.B. eine arithmetisch wachsende Rente) folgt. Rentenzahlungen zu Beginn (zum Ende) der Periode werden als vorschüssig (nachschüssig) bezeichnet. Bezüglich der Länge des Zeitraums ist zwischen einer endlichen und einer unendlichen (ewigen) Rente zu unterscheiden. Analog zu den Varianten einer jährlichen Rente sind Modelle mit unterjähriger Rente gestaltbar. Bei ihnen kann der Renten- und Zinszahlungszeitpunkt auseinanderfallen. Der Zinsfuß wird im Allgemeinen für den gesamten Zeitraum der Rentenzahlungen als konstant angenommen.
Mit Hilfe der Rentenrechnung kann der auf einen bestimmten Zeitpunkt bezogene Wert einer Rente bestimmt werden. Wird als Bezugszeitpunkt der Anfangszeitpunkt der Rente gewählt, so ist vom Rentenbarwert zu sprechen, werden die Rentenzahlungen auf das Ende des gesamten Zeitraums aufgezinst, so stellt der entsprechende Wert den Rentenendwert dar. Falls der Bar- bzw. Endwert vorgegeben wird, kann bei festliegendem Zeitraum und Zinssatz die Höhe der Rente bestimmt werden. Analog sind Zinssatz respektive Rentenzeitraum zu errechnen.
2. Standardansätze a) Endliche Rente
Der Standardansatz einer endlichen Rente sei durch eine konstante Rente, die ebenso wie die Zinszahlungen am Ende eines jeden Jahres anfällt, gekennzeichnet. Der Zinsfuß ist während der gesamten Laufzeit konstant. Der Rentenendwert kann in diesem Fall wie folgt bestimmt werden:
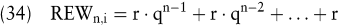
REWn,i Rentenendwert für eine Rente mit der Laufzeit n bei einem Zinssatz von i
r Rente
q Zinsfaktor 1 + i
Die Formel zur Bestimmung des Rentenendwertes stellt eine geometrisch-fallende Reihe dar, die durch einige mathematische Operationen zu folgendem kompakten Ausdruck umgeformt werden kann:
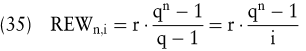
Der Rentenendwert ergibt sich also durch Multiplikation der Rente r mit dem sog. Rentenendwertfaktor.
Der Rentenbarwert RBWn,i kann analog ermittelt werden. Er ist wie folgt definiert:
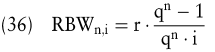
Der reziproke Rentenbarwertfaktor wird auch als Wiedergewinnungsfaktor bezeichnet.
Falls Renten- und Zinszahlungen ertragsteuerlich relevant sind, ist eine Modifikation des Grundmodells erforderlich, um Rentenendwert bzw. -barwert nach Steuern zu bestimmen. Die Korrekturen der Rente und der Zinsen ist am Beispiel des Standardansatzes der Endwertbestimmung einer endlichen Rente darzustellen:
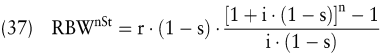
In der obigen Formel stellt s den marginalen Steuersatz dar.
Die Implikationen seien durch ein Beispiel verdeutlicht. Angenommen, eine Unternehmung verpachte ein Grundstück und erhalte dafür drei Jahre lang jährlich nachschüssig 1.000 EUR. Aus finanzmathematischer Sicht ist diese Pacht als Rente zu betrachten. Um deren Endwert zu bestimmen, sei angenommen, die Pacht würde jeweils zeitgleich zum Zinssatz von 8% angelegt. Als marginaler Steuersatz sei 60% unterstellt. Der aufgrund der oben dargestellten „ Rentenendwertformel nach Steuern “ ermittelte Wert von 1.238,75 EUR kann in einem VOFI visualisiert werden. 
Abb. 5: VOFI zur Rentenrechnung mit Steuern
b) Ewige Rente
Bei einer ewigen Rente sind die Rentenzahlungszeitpunkte unbegrenzt. Im Standardansatz der ewigen Rente wird angenommen, dass Zins- und Ratenzahlungen jährlich zeitgleich in nachschüssiger Form erfolgen. Außerdem ist der Zinsfuß konstant.
Während der Endwert einer ewigen Rente offenbar unendlich hoch ist, weist ihr Barwert wegen des Zinseffektes einen endlichen Wert auf, der sich aufgrund einer Grenzwertbetrachtung für n -> ∞ wie folgt ergibt:
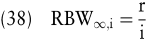
Das Modell der ewigen Rente ist beispielsweise in der klassischen Theorie der optimalen Nutzungsdauer von Investitionsprojekten relevant, wenn im Modell unendlich viele mit der Anfangsinvestition identische Folgeinvestitionen unterstellt werden (Hax, H. 1993). Aber auch bei einer finanzplanorientierten Investitionsrechnung wird der Barwert einer unendlichen vieler Rente benötigt. Er ist unter der Bedingung unendlich vieler identischer Folgeinvestitionen bei der Bewertung der jenseits des Planungshorizonts liegenden Aktivitäten anzusetzen (Grob, H. L. 2001).
3. Variationen zu den Standardansätzen
Neben den oben erörterten Ansätzen wird in der Literatur eine Vielzahl von Varianten der Rentenrechnung behandelt, die sich insbesondere auf Fragen der Unterjährigkeit und der gleichmäßigen oder intervallweisen Dynamisierung der Rente beziehen (Bosch, K. 1998; Kruschwitz, L. 1995).
VI. PC-Anwendungen
Fragestellungen zur Zins-, Tilgungs- und Rentenrechnung können mit Hilfe von PC-Programmen einfach gelöst werden. Für Standardfälle und ihre Variationen existiert eine Reihe von Anwendungsprogrammen. Auch werden in Tabellenkalkulationsverfahren die wichtigsten finanzmathematischen Formeln als Funktionen zur Verfügung gestellt.
Für nicht standardmäßige Fragestellungen können Tabellenkalkulationsverfahren eingesetzt werden, in denen anstelle einer geschlossenen formelmäßigen Abbildung eine deskriptive Problemlösung durch Erarbeiten von Arbeitsblättern ( „ Spreadsheets “ ) erfolgt. Sensitivitätsanalysen sowie die Bestimmung kritischer Werte (z.B. von Effektivzinsfüßen) werden durch diese finanzplanorientierten Methoden wirkungsvoll unterstützt.
Literatur:
Bosch, K. : Finanzmathematik, 5. A., München 1998
Forster, O. : Analysis 1, 5. A., Heidelberg 1993
Grob, H. L. : Einführung in die Investitionsrechnung, 4. A., München 2001
Hass, O. : Finanzmathematik – finanzmathematische Methoden der Investitionsrechnung, 6. A., München, Wien 2000
Hax, H. : Investitionstheorie, 5. A., Heidelberg 1993
Kobelt, H./Schulte, P. : Finanzmathematik, Methoden, betriebswirtschaftliche Anwendungen und Aufgaben mit Lösungen, 7. A., Herne 1999
Kosiol, E. : Finanzmathematik, Zinseszins-, Renten-, Tilgungs-, Kurs- und Rentabilitätsrechnung, 10. A., Wiesbaden 1984
Kruschwitz, L. : Finanzmathematik, Lehrbuch der Zins-, Renten-, Tilgungs-, Kurs- und Renditerechnung, 2. A., München 1995
Perridon, L./Steiner, M. : Finanzwirtschaft der Unternehmung, 10. A., München 1999
Wimmer, K. : Finanzmathematik: Grundlagen und Anwendungsmöglichkeiten in der Investitions- und Bankwirtschaft, begr. von Caprano, E./, ab der 6. A. fortgef. von Wimmer, K., 6. A., München 1999
|